React Diff算法深度解析

Diff算法的核心挑战

传统树比较的复杂度问题

传统的树比较算法（如Tree Edit Distance）时间复杂度为O(n³)，其中n是树的节点数量。对于大型应用来说，这种复杂度是完全不可接受的。

1
2
3
4
5
6
// 传统树编辑距离算法伪代码
function treeEditDistance(tree1, tree2) {
  // 时间复杂度：O(n³)
  // 空间复杂度：O(n²)
  // 对于React规模的应用程序来说过于昂贵
}

React的优化策略

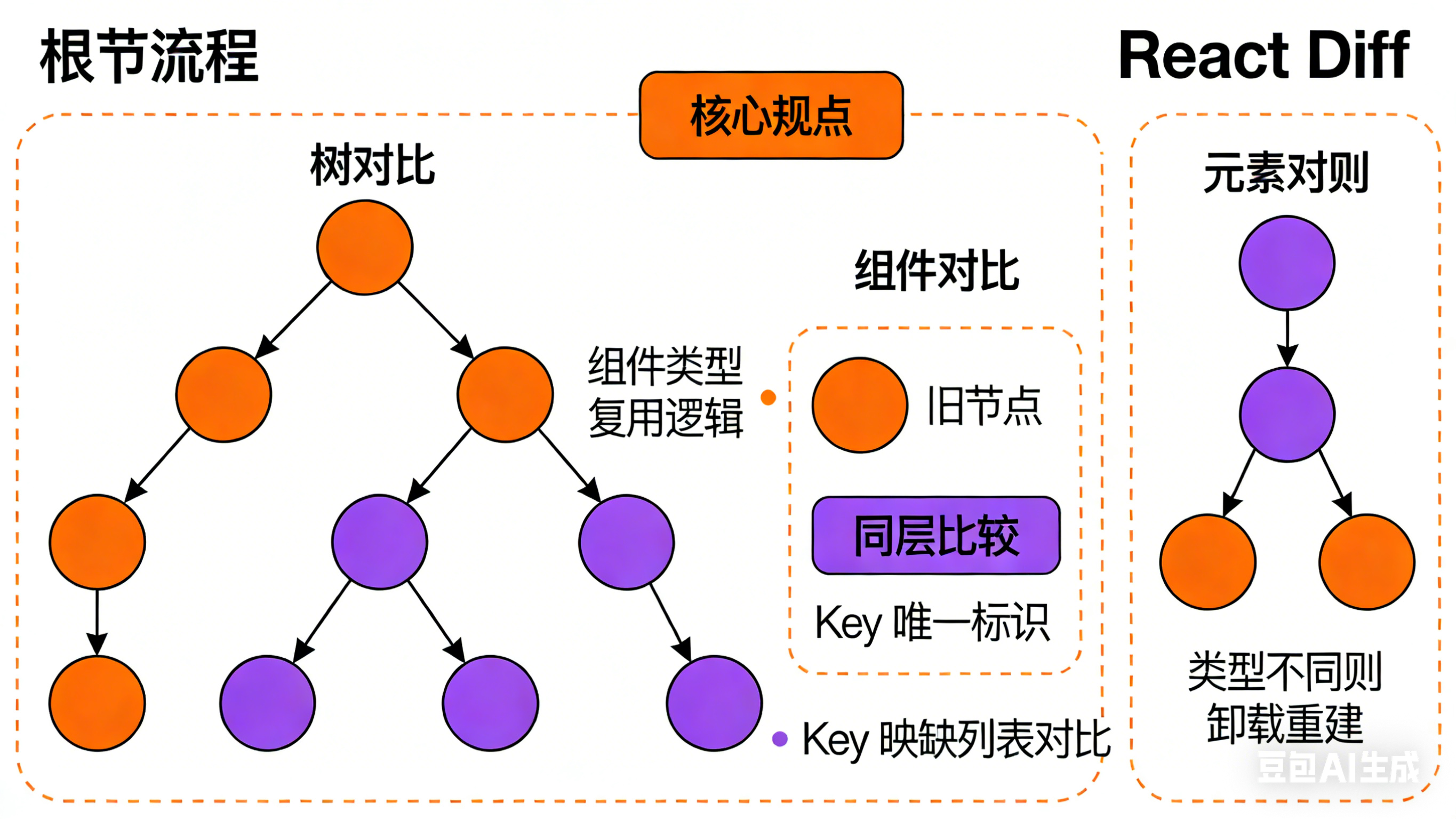
React通过以下启发式规则将复杂度降低到O(n)：

  1. 类型不同则完全替换：如果元素类型不同，直接替换整个子树
  2. 键值标识元素：通过key属性识别元素的移动和复用
  3. 同级比较：只在同级元素间进行比较，不跨层级

Diff算法的三层比较策略

1. 树层级比较（Tree Level）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function diffTrees(oldTree, newTree) {
  // 如果根节点类型不同，直接替换整个树
  if (oldTree.type !== newTree.type) {
    return { type: 'REPLACE', newTree };
  }
  
  // 比较属性
  const propPatches = diffProps(oldTree.props, newTree.props);
  
  // 比较子节点
  const childPatches = diffChildren(
    oldTree.props.children,
    newTree.props.children
  );
  
  return { type: 'UPDATE', propPatches, childPatches };
}

2. 组件层级比较（Component Level）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function shouldUpdateComponent(prevElement, nextElement) {
  // 类型不同，需要更新
  if (prevElement.type !== nextElement.type) {
    return true;
  }
  
  // key不同，需要更新
  if (prevElement.key !== nextElement.key) {
    return true;
  }
  
  // props深度比较
  return !shallowEqual(prevElement.props, nextElement.props);
}

3. 元素层级比较（Element Level）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
function diffChildren(oldChildren, newChildren) {
  const patches = [];
  const oldMap = createKeyToOldIdxMap(oldChildren);
  
  let newIdx = 0;
  let lastPlacedIndex = 0;
  
  // 第一遍：遍历新节点
  while (newIdx < newChildren.length) {
    const newChild = newChildren[newIdx];
    const oldIdx = oldMap[newChild.key];
    
    if (oldIdx === undefined) {
      // 新节点，需要插入
      patches.push(createInsertPatch(newChild, newIdx));
    } else {
      //  existing节点，可能移动
      const oldChild = oldChildren[oldIdx];
      if (shouldUpdateElement(oldChild, newChild)) {
        patches.push(createUpdatePatch(oldChild, newChild, newIdx));
      }
      
      // 检查移动情况
      if (oldIdx < lastPlacedIndex) {
        patches.push(createMovePatch(newChild, newIdx));
      }
      lastPlacedIndex = Math.max(oldIdx, lastPlacedIndex);
    }
    
    newIdx++;
  }
  
  // 第二遍：删除旧节点中不存在的节点
  // ... 省略删除逻辑
  
  return patches;
}

Key的重要性和实现原理

Key的作用机制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function createKeyToOldIdxMap(children) {
  const map = {};
  for (let i = 0; i < children.length; i++) {
    const child = children[i];
    if (child.key != null) {
      if (map[child.key] !== undefined) {
        // 重复key警告
        console.warn('Duplicate keys detected:', child.key);
      }
      map[child.key] = i;
    }
  }
  return map;
}

Key的最佳实践

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 错误：使用索引作为key（当列表顺序可能变化时）
const badList = items.map((item, index) => (
  <Item key={index} item={item} />
));

// 正确：使用唯一稳定标识作为key
const goodList = items.map(item => (
  <Item key={item.id} item={item} />
));

// 正确：对于没有id的静态列表，可以使用索引
const staticList = staticItems.map((item, index) => (
  <Item key={index} item={item} />
));

列表Diff的详细算法

最长递增子序列（LIS）优化

React使用最长递增子序列算法来最小化DOM操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
function findLongestIncreasingSubsequence(arr) {
  const piles = [];
  const sequence = [];
  
  for (let i = 0; i < arr.length; i++) {
    const num = arr[i];
    let left = 0;
    let right = piles.length;
    
    // 二分查找插入位置
    while (left < right) {
      const mid = Math.floor((left + right) / 2);
      if (piles[mid] < num) {
        left = mid + 1;
      } else {
        right = mid;
      }
    }
    
    if (left < piles.length) {
      piles[left] = num;
    } else {
      piles.push(num);
    }
    
    sequence[i] = left > 0 ? sequence[left - 1] : -1;
  }
  
  // 构造LIS
  const lis = [];
  let current = piles.length - 1;
  for (let i = arr.length - 1; i >= 0; i--) {
    if (sequence[i] === current) {
      lis.unshift(arr[i]);
      current--;
    }
  }
  
  return lis;
}

移动检测算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function calculateMoves(oldIndices, newIndices) {
  const moves = [];
  const source = oldIndices.slice();
  const dest = newIndices.slice();
  
  // 标记不需要移动的元素
  const lis = findLongestIncreasingSubsequence(dest);
  const shouldMove = new Array(dest.length).fill(true);
  
  for (const index of lis) {
    shouldMove[index] = false;
  }
  
  // 生成移动操作
  for (let i = dest.length - 1; i >= 0; i--) {
    if (shouldMove[i]) {
      moves.push({
        type: 'MOVE',
        from: source.indexOf(dest[i]),
        to: i
      });
    }
  }
  
  return moves;
}

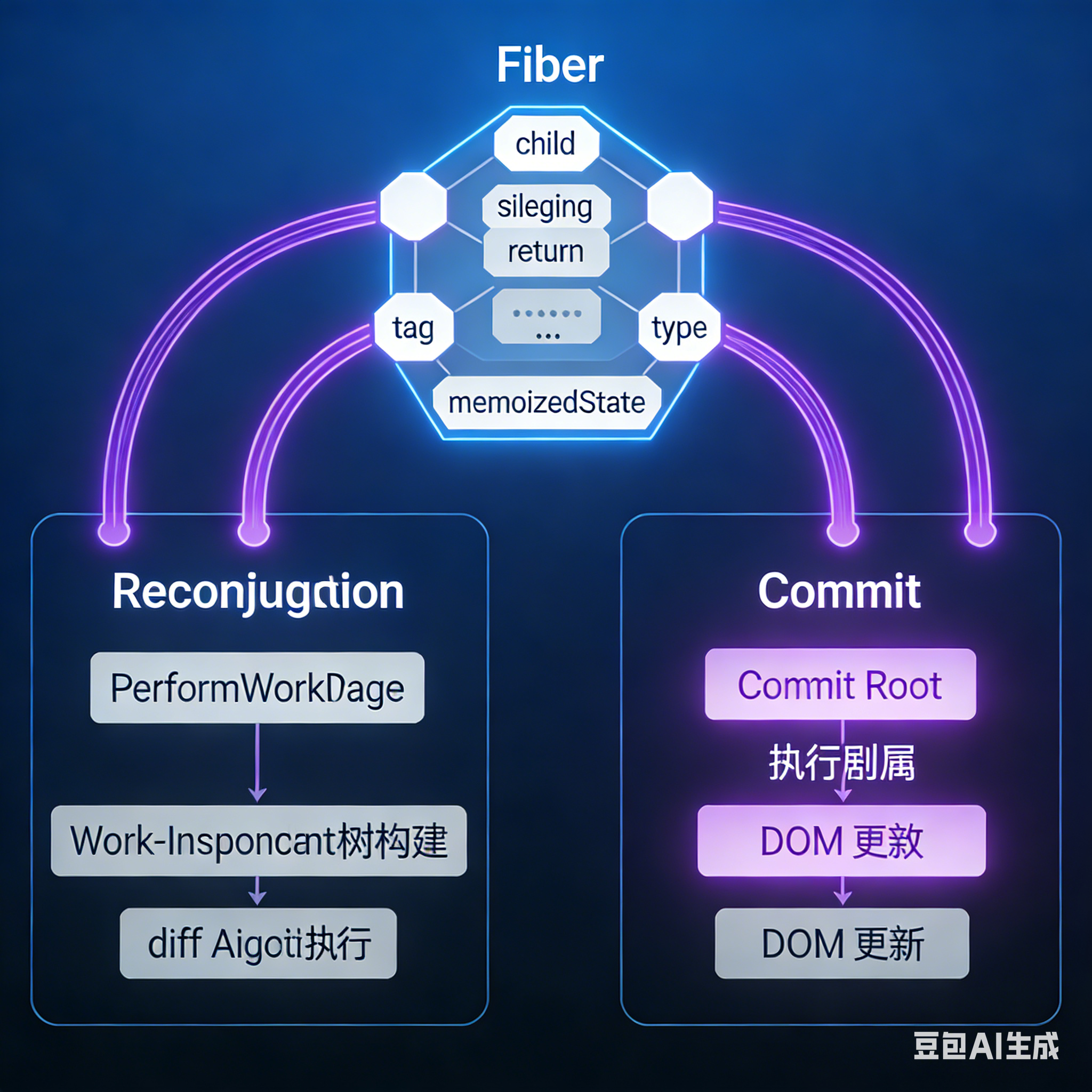
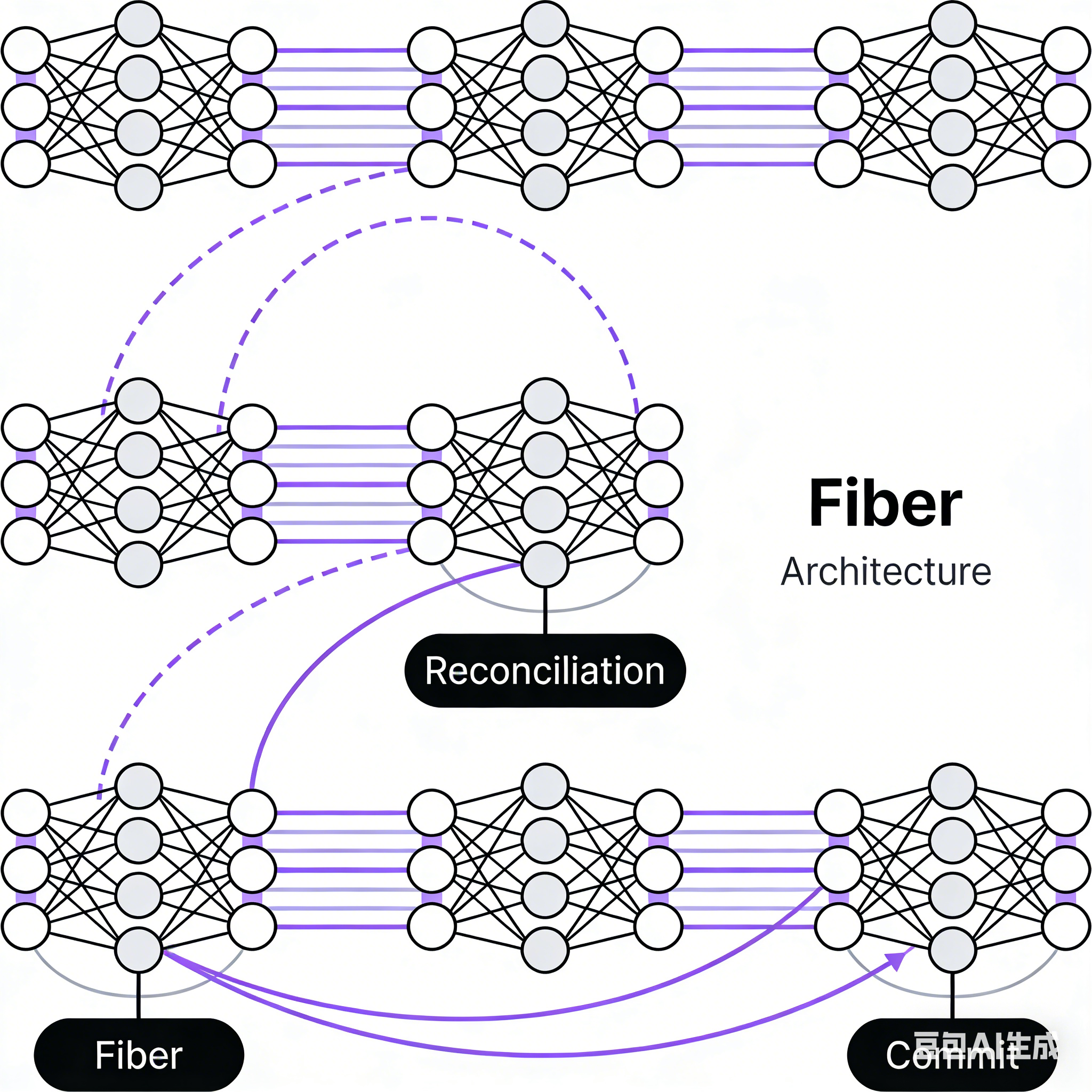
Fiber架构中的Diff实现

双缓存技术的Diff

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
function reconcileChildFibers(
  returnFiber,
  currentFirstChild,
  newChildren,
  lanes
) {
  // 处理不同类型的子节点
  if (typeof newChildren === 'object' && newChildren !== null) {
    switch (newChildren.$$typeof) {
      case REACT_ELEMENT_TYPE:
        return placeSingleChild(
          reconcileSingleElement(
            returnFiber,
            currentFirstChild,
            newChildren,
            lanes
          )
        );
      case REACT_PORTAL_TYPE:
        return placeSingleChild(
          reconcileSinglePortal(
            returnFiber,
            currentFirstChild,
            newChildren,
            lanes
          )
        );
      default:
        // 处理数组或迭代器
        if (isArray(newChildren)) {
          return reconcileChildrenArray(
            returnFiber,
            currentFirstChild,
            newChildren,
            lanes
          );
        }
        // ... 其他类型处理
    }
  }
  
  // 文本节点处理
  if (typeof newChildren === 'string' || typeof newChildren === 'number') {
    return placeSingleChild(
      reconcileSingleTextNode(
        returnFiber,
        currentFirstChild,
        '' + newChildren,
        lanes
      )
    );
  }
  
  // 空节点处理
  return deleteRemainingChildren(returnFiber, currentFirstChild);
}

单元素Diff

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function reconcileSingleElement(
  returnFiber,
  currentFirstChild,
  element,
  lanes
) {
  const key = element.key;
  let child = currentFirstChild;
  
  while (child !== null) {
    // 首先比较key
    if (child.key === key) {
      // key匹配，比较type
      if (child.type === element.type) {
        // 类型相同，可以复用
        deleteRemainingChildren(returnFiber, child.sibling);
        const existing = useFiber(child, element.props);
        existing.return = returnFiber;
        return existing;
      } else {
        // 类型不同，删除所有旧子节点
        deleteRemainingChildren(returnFiber, child);
        break;
      }
    } else {
      // key不匹配，删除当前子节点
      deleteChild(returnFiber, child);
    }
    child = child.sibling;
  }
  
  // 创建新Fiber
  const created = createFiberFromElement(element, returnFiber.mode, lanes);
  created.return = returnFiber;
  return created;
}

性能优化策略

shouldComponentUpdate的优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class OptimizedComponent extends React.Component {
  shouldComponentUpdate(nextProps, nextState) {
    // 浅比较props和state
    return !shallowEqual(this.props, nextProps) ||
           !shallowEqual(this.state, nextState);
  }
  
  render() {
    return <div>{this.props.value}</div>;
  }
}

// 使用React.memo进行函数组件优化
const MemoizedComponent = React.memo(function MyComponent(props) {
  return <div>{props.value}</div>;
}, (prevProps, nextProps) => {
  // 自定义比较函数
  return prevProps.value === nextProps.value;
});

不可变数据结构的优势

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 使用不可变数据结构优化Diff
import { produce } from 'immer';

function reducer(state, action) {
  return produce(state, draft => {
    switch (action.type) {
      case 'UPDATE_ITEM':
        // 直接修改draft，immer会处理不可变更新
        draft.items[action.index] = action.item;
        break;
      case 'ADD_ITEM':
        draft.items.push(action.item);
        break;
    }
  });
}

// 使用Immutable.js
import { List } from 'immutable';

const list1 = List([1, 2, 3]);
const list2 = list1.push(4); // 创建新引用，原list1不变

// React可以快速判断引用是否变化
if (list1 !== list2) {
  // 需要更新
}

Diff算法的局限性

算法假设的局限性

  1. 相同类型的组件：假设产生相似的树结构
  2. Key的稳定性：假设key在整个生命周期中稳定不变
  3. 同级比较：无法处理跨层级的移动

边缘情况处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 处理无效的key情况
function validateKeys(children) {
  const keys = {};
  React.Children.forEach(children, (child, index) => {
    if (child.key != null) {
      if (keys[child.key]) {
        console.error(
          'Duplicate keys detected: ' + child.key +
          '. This can cause performance issues in React.'
        );
      }
      keys[child.key] = true;
    }
  });
}

// 处理动态key生成
function generateStableKey(item, index) {
  // 避免使用不稳定的key
  if (item.id) return item.id;
  if (item.name) return item.name;
  
  // 最后才使用索引，并添加前缀避免冲突
  return `index-${index}`;
}

实战：实现简易Diff算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
class SimpleDiff {
  static diff(oldChildren, newChildren) {
    const patches = [];
    const oldMap = this.createKeyMap(oldChildren);
    let newIndex = 0;
    let lastPlacedIndex = 0;
    
    // 第一遍：处理新children
    while (newIndex < newChildren.length) {
      const newChild = newChildren[newIndex];
      const oldIndex = oldMap[newChild.key];
      
      if (oldIndex === undefined) {
        // 新增节点
        patches.push({
          type: 'INSERT',
          node: newChild,
          index: newIndex
        });
      } else {
        // 现有节点
        const oldChild = oldChildren[oldIndex];
        
        // 检查是否需要更新
        if (!this.isSameNode(oldChild, newChild)) {
          patches.push({
            type: 'UPDATE',
            oldNode: oldChild,
            newNode: newChild,
            index: newIndex
          });
        }
        
        // 检查是否需要移动
        if (oldIndex < lastPlacedIndex) {
          patches.push({
            type: 'MOVE',
            from: oldIndex,
            to: newIndex
          });
        }
        
        lastPlacedIndex = Math.max(oldIndex, lastPlacedIndex);
        delete oldMap[newChild.key];
      }
      
      newIndex++;
    }
    
    // 第二遍：删除旧children中剩余的节点
    Object.values(oldMap).forEach(oldIndex => {
      patches.push({
        type: 'DELETE',
        index: oldIndex
      });
    });
    
    return patches;
  }
  
  static createKeyMap(children) {
    const map = {};
    children.forEach((child, index) => {
      if (child.key != null) {
        map[child.key] = index;
      }
    });
    return map;
  }
  
  static isSameNode(a, b) {
    return a.type === b.type && a.key === b.key;
  }
}

React 18中的Diff改进

并发模式下的Diff

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function reconcileChildrenConcurrent(
  current,
  workInProgress,
  nextChildren,
  renderLanes
) {
  // 并发模式下的Diff算法
  if (current === null) {
    // 挂载阶段
    workInProgress.child = mountChildFibers(
      workInProgress,
      null,
      nextChildren,
      renderLanes
    );
  } else {
    // 更新阶段
    workInProgress.child = reconcileChildFibers(
      workInProgress,
      current.child,
      nextChildren,
      renderLanes
    );
  }
}

渐进式Hydration

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function hydrateRoot(container, element) {
  // 渐进式水合，支持部分Hydration
  const root = createRoot(container, {
    hydrate: true,
    hydrationCallbacks: {
      onHydrated: (suspenseInstance) => {
        console.log('Component hydrated:', suspenseInstance);
      },
      onDeleted: (suspenseInstance) => {
        console.log('Component deleted:', suspenseInstance);
      }
    }
  });
  
  root.render(element);
  return root;
}

测试和调试

Diff算法的单元测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
describe('React Diff Algorithm', () => {
  test('should handle element reordering', () => {
    const oldChildren = [
      { key: 'a', type: 'div' },
      { key: 'b', type: 'div' },
      { key: 'c', type: 'div' }
    ];
    
    const newChildren = [
      { key: 'c', type: 'div' },
      { key: 'a', type: 'div' },
      { key: 'b', type: 'div' }
    ];
    
    const patches = SimpleDiff.diff(oldChildren, newChildren);
    
    expect(patches).toContainEqual({
      type: 'MOVE',
      from: 2, // 'c'的旧位置
      to: 0    // 'c'的新位置
    });
  });
  
  test('should detect element updates', () => {
    const oldChildren = [{ key: 'a', type: 'div', props: { className: 'old' } }];
    const newChildren = [{ key: 'a', type: 'div', props: { className: 'new' } }];
    
    const patches = SimpleDiff.diff(oldChildren, newChildren);
    
    expect(patches).toContainEqual({
      type: 'UPDATE',
      oldNode: expect.any(Object),
      newNode: expect.any(Object),
      index: 0
    });
  });
});

性能分析和调试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 使用React DevTools Profiler分析Diff性能
function ExpensiveList() {
  const items = useMemo(() => 
    Array.from({ length: 1000 }, (_, i) => ({ id: i, value: Math.random() }))
  , []);
  
  return (
    <div>
      {items.map(item => (
        <ExpensiveItem key={item.id} item={item} />
      ))}
    </div>
  );
}

// 使用why-did-you-render调试不必要的重渲染
whyDidYouRender(React, {
  trackAllPureComponents: true,
  trackHooks: true,
  logOnDifferentValues: true
});

最佳实践总结

1. 键值策略

1
2
3
4
5
6
7
8
// ✅ 使用稳定唯一的标识符
<Item key={item.id} />

// ❌ 避免使用索引（除非列表完全静态）
<Item key={index} />

// ❌ 绝对不要使用随机数
<Item key={Math.random()} />

2. 组件设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// ✅ 使用PureComponent或React.memo
class OptimizedComponent extends React.PureComponent {
  render() {
    return <div>{this.props.value}</div>;
  }
}

// ✅ 使用useMemo和useCallback
function OptimizedComponent({ items }) {
  const memoizedItems = useMemo(() => items.map(processItem), [items]);
  const handleClick = useCallback(() => {
    // 处理点击
  }, []);
  
  return <div onClick={handleClick}>{memoizedItems}</div>;
}

3. 数据结构优化

1
2
3
4
5
6
7
8
// ✅ 使用不可变数据结构
const newState = {
  ...state,
  items: [...state.items, newItem]
};

// ✅ 使用扁平化数据结构
// 而不是嵌套过深的对象

结论

React的Diff算法通过巧妙的启发式规则和优化策略，成功将树比较的复杂度从O(n³)降低到O(n)。